728x90
https://www.acmicpc.net/problem/11444
11444번: 피보나치 수 6
첫째 줄에 n이 주어진다. n은 1,000,000,000,000,000,000보다 작거나 같은 자연수이다.
www.acmicpc.net
#include<iostream>
#include<vector>
using namespace std;
typedef long long ll;
typedef vector<vector<ll>> matrix;
#define DIVMOD 1000000007;
matrix operator *(matrix a, matrix b) {
ll i, j, k;
matrix ret(2, vector<ll>(2));
for (i = 0; i < a.size(); ++i)
{
for (j = 0; j < a.size(); ++j)
{
for (k = 0; k < a.size(); ++k)
{
ret[i][j] += (a[i][k] * b[k][j]);
}
ret[i][j] %= DIVMOD;
}
}
return ret;
}
matrix findFibo(ll num) {
matrix base_matrix(2, vector<ll>(2, 1));
base_matrix[1][1] = 0;
if (num < 2) {
return base_matrix;
}
matrix ret(2, vector<ll>(2));
ret = findFibo(num / 2);
if (num % 2) {
return ret * ret * base_matrix;
} else {
return ret * ret;
}
}
int main() {
ll n;
cin >> n;
matrix ans = findFibo(n-1);
cout << ans[0][0] << endl;
return 0;
}피보나치 문제가 왜 분할정복인지 몰랐는데 분할정복을 사용해야만 시간초과가 걸리지 않는다.

아래는 위의 행렬을 도출하는 수식이다.
더보기




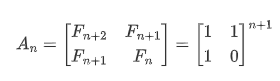
분할정복으로 풀기위해선 피보나치의 점화식을 행렬로 표현해야한다.

여기에서 다음과 같이 더 확장 할수 있다.

각 행렬을 An으로 치환하면 다음과 같이 나타낼수 있다.

A0 가 {1,1,1,0}이므로 An은 {1,1,1,0}의 n 거듭제곱 꼴로 나타낼수 있다.

An을 다시 치환하면 다음과 같은 식을 얻는다
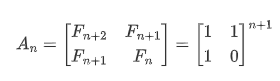
분할정복 알고리즘 자체는 어렵지 않지만 어떻게 분할해야할지가 가장 핵심인듯하다.
'STUDY > Algorithm' 카테고리의 다른 글
| [프로그래머스] 해시 level3 베스트 앨범, python (0) | 2021.12.26 |
|---|---|
| [백준] 1504 특정한 최단경로 python (0) | 2021.12.24 |
| [백준] 10830 행렬제곱 C++ (0) | 2021.12.10 |
| [백준] 1966 프린터 큐 C (0) | 2021.11.29 |
| [백준] 18258 큐2 C (0) | 2021.11.29 |